Велика теорема Ферма

10.01.2016 15:59

Велика теорема Ферма

Ferma.png

Велика теорема Ферма (відома теорема Ферма, остання теорема Ферма) — твердження, що для довільного натурального числа 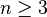n\geq 3 рівняння x^n+y^n=z^n\!(рівняння Ферма) не має розв´язків у цілих числах \ x, y, z, відмінних від нуля.

Вона була сформульована приблизно в 1637 році французьким математиком П'єром Ферма на берегах книги Діофанта «Арифметика» таким чином:

 
Видання 1670 року «Арифметики» Діофанта включає коментар Ферма, зокрема його «велику теорему» (Observatio Domini Petri de Fermat).

«Неможливо розкласти ні куб на два куби, ні біквадрат на два біквадрати, ні взагалі довільний степінь, більший від квадрата, на два степені з еквівалентним показником. Я відкрив цьому воістину чудове доведення, але ці поля для нього занадто малі».

Історія доведення

Пізніше Ферма опублікував доведення для випадку n=4, що дає підстави для сумнівів, чи було у нього доведення для загального випадку.

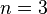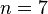Ейлер в 1770 році довів теорему для випадку n=3, Діріхле та Лежандр в 1825 — для n=5, Габрієль Ламе — для n=7. Ернст Куммер довів, що теорема справедлива для всіх простих n, менших за 100, за можливим винятком так званих іррегулярних простих 37, 59, 67.

Нездоровий інтерес до теореми Ферма серед неспеціалістів був викликаний великою грошовою премією Вольфскеля за її доведення, але через інфляцію після Першої світової війни, премія значно знизилася.

Доведення теореми було завершене у вересні 1994 року Ендрю Вайлсом. 129-сторінкове доведення було надруковане у журналі «Annals of Mathematics»[1] у 1995 році, втім у ньому було знайдено значну прогалину, й остаточне доведення теореми було здійснене у 1995 р. Ендрю Вайлсом за участі Лоуренса Тейлора.

Назад