Головна сторінка > Теореми Банаха

Теореми Банаха

10.01.2016 13:45

Теорема Банаха про замкнений графік

Нехай X, Y — банахові простори над одним і тим же полем, L — підпростір простору X. Для того, щоб лінійний оператор $A:L\to Y$ був неперервним, необхідно і достатньо, щоб його графік $\Gamma _{A}$ був замкнений в декартовому добутку $X\times Y$ (якщо його розглядати як нормований простір).

Теорема про замкнений графік зокрема говорить, що графік неперервної функції, означеної на замкненій множині, є множиною замкненою.

Теорема Банаха про нерухому точку

Ця теорема була сформульована і доведена у 1922 році Стефаном Банахом. Вона є однією з найбільш класичних і фундаментальних теорем функціонального аналізу, а тому її результати використовуються при доведенні багатьох інших тверджень цієї дисципліни.

Всяке стискуюче відображення повного метричного простору в себе має єдину нерухому точку (яку можна знайти методом послідовних наближень, починаючи з будь-якої точки цього простору).

Нехай (X,d) — метричний простір, $A:X\to X$ — відображення метричного простору X в себе, тоді існує єдиний елемент

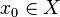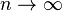x метричного простору X, що при відображенні A переходить в себе, тобто A(x)=x. Для того, щоб знайти цей елемент, можна побудувати таку послідовність. Потрібно взяти довільний елемент $x_0\in X$ , потім покласти $x_1=A(x_0)$ після цього взяти $x_2=A(x_1)$ далі $x_3=A(x_2)$ і так далі. Отрималась послідовність $(x_n)$ яка прямує до шуканого елемента x (при $n\to \infty$ ).