Головна сторінка > Теорема Гамільтона — Келі

Теорема Гамільтона — Келі

10.01.2016 16:01

Теорема Гамільтона — Келі

Теоре́ма Га́мільтона — Ке́лі (на честь Вільяма Гамільтона та Артура Келі) стверджує, що результат підстановки квадратної матриці $A$ до її характеристичного полінома тотожно дорівнює нулю:

\ p_A(A)=0.

Теорема Гамільтона-Келі дозволяє виразити поліноми високого степеня від $n\times n$ матриці $A$ як лінійні комбінації $A^{n-1},\ldots,A,I.$

Оскільки результатом додавання, множення та множення на скаляр квадратних матриць є квадратна матриця, то можна конструювати поліноми з матриць.

Тому для довільного полінома $\ f(x)=a_0 x^k+a_1 x_{k-1}+\ldots+a_{k-1}x+a_k$ можливо розглянути вираз

\ f(A)=a_0 A^k+a_1 A^{k-1}+\ldots+a_{k-1} A+a_k I,

який є квадратною матрицею того самого порядка, що й 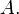$A.$

Приклад[ред. • ред. код]

A=\begin{bmatrix}0 & 1\\2 & 3\end{bmatrix}, \quad p_A(\lambda)=\lambda^2-3\lambda-2.

Тоді $A^2=\begin{bmatrix}0 & 1\\2 & 3\end{bmatrix}\begin{bmatrix}0 & 1\\2 & 3\end{bmatrix}=\begin{bmatrix}2 & 3\\6 & 11\end{bmatrix}, \qquad p_A(A)=A^2-3A-2I=\begin{bmatrix}2 & 3\\6 & 11\end{bmatrix}-\begin{bmatrix}0 & 3\\6 & 9\end{bmatrix}-\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix}=\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}.$

Часткові випадки[ред. • ред. код]

Доведемо теорему для матриць 2x2.

Маємо $A=\begin{bmatrix}a & b\\c & d\end{bmatrix}, \quad p_A(\lambda)=\lambda^2-(\operatorname{tr}A)\lambda+(\det A),$ тому

$p_A(A)=A^2-(a+d)A+(ad-bc)I = \begin{bmatrix}a^2+bc & ab+bd\\ ca+dc & cb+d^2\end{bmatrix}-\begin{bmatrix}(a+d)a & (a+d)b\\ (a+d)c & (a+d)d\end{bmatrix}+\begin{bmatrix}ad-bc & 0\\0 & ad-bc\end{bmatrix}=\begin{bmatrix}0 & 0\\0 & 0\end{bmatrix}.$

Розглянемо випадок діагональних матриць.

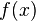Якщо $A=\operatorname{diag}(\lambda_1,\ldots,\lambda_n)$ — діагональна матриця і $\ f(x)$ — поліном, то

f(A)=\operatorname{diag}(f(\lambda_1),\ldots,f(\lambda_n)).

Для характеристичного полінома $\ p_A(\lambda_1)=\ldots=p_A(\lambda_n)=0,$ тому одержуємо $p_A(A)= \operatorname{diag}(0,\ldots,0).$

Загальний випадок[ред. • ред. код]

Позначимо через $\ B$ союзну матрицю для характеристичної матриці $\ \lambda I_n-A.$

Елементи матриці В є алгебраїчними доповненнями елементів визначника $\lambda I_n-A,$ і тому є многочленами від λ, степені не вище n-1. Отже матрицю В можна представити у вигляді полінома з матричними коефіцієнтами: