Теорема Блоха

10.01.2016 14:02

Теорема Блоха

Теорема Блоха — одне із основних тверджень квантової теорії ідеальних кристалів, яке задає загальний вигляд хвильових функцій електронних станів у твердому тілі з трансляційною симетрією.

У періодичному кристалі з періодом  \mathbf{a}  електронні стани мають хвильові функції виду

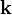\psi_{\mathbf{k}}(\mathbf{r}) = v_k(\mathbf{r}) e^{i\mathbf{kr}},

де  v_k(\mathbf{r}) = v_k(\mathbf{r}+\mathbf{a})  є певною періодичною функцією із періодом  \mathbf{a} .

Вектор  \mathbf{k}  називається хвильовим вектором.

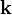Якщо  \mathbf{K}  є вектором оберненої ґратки, то функція  e^{i\mathbf{Kr}}, теж є періодичною, а значить хвильовий вектор  \mathbf{k} - \mathbf{K}  теж задовольняє теоремі Блоха. Ця обставина створює умови для того, щоб вибирати хвильові вектори лише в першій зоні Брілюена, віднімаючи від будь-якого  \mathbf{k}  вектор оберненої ґратки необхідну кількість разів.

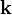Величину  \hbar\mathbf{k} , коли  \mathbf{k}  приведено до першої зони Брілюена називають квазі-імпульсом, щоб відрізнити від звичайного імпульсу, який може приймати будь-яке значення.

Квазі-імпульс можна вибрати квантовим числом одноелектронного стану. Відповідно, говорять, що такий стан характеризує квазічастинку.

 

Назад