У теорії ймовірностей та статистиці Теоре́ма Ба́єса (або ж Зако́н Ба́єса, чи Правило Баєса) визначає співвідношення поточної ймовірності до попередньої. Вона є важливою в математичному маніпулюванні умовними ймовірностями.

При застосуванні, задіяні у теоремі Баєса ймовірності можуть мати різні інтерпретації. В одній із цих інтерпретацій теорема Баєса використовується безпосередньо у певному підході до статистичного виведення. Зокрема, при баєсовій інтерпретації ймовірності ця теорема виражає, як повинна раціонально змінюватися суб'єктивна міра впевненості при врахуванні свідчення: це є баєсовим виведенням, що є фундаментальним для баєсової статистики. Тим не менш, теорема Баєса має численні застосування у широкому спектрі обчислень із залученням ймовірностей, а не лише у баєсовому виведенні.

Теорему Баєса названо на честь прп. Томаса Баєса ([ˈbeɪz]; 1701–1761), який першим показав, як використовувати свідчення для уточнення переконань. Її було розвинуто далі П'єром-Симоном Лапласом, який вперше опублікував це сучасне формулювання у своїй праці 1812 року «Аналітична теорія ймовірностей». Сер Гарольд Джеффріс поклав баєсів алгоритм та лапласове формулювання на аксіоматичну основу. Деффріс писав, що теорема Баєса «є для теорії ймовірностей тим, чим теорема Піфагора є для геометрії».

Теорема Баєса задається математично наступним рівнянням:

,

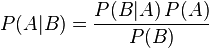де  та  є подіями.

•  та  є ймовірностями  та  незалежно одна від одної.
• , умовна ймовірність, є ймовірністю  за умови істинності .
•  є ймовірністю  за умови істинності .